Sistemas de Particulas

Dinámica de un sistema de partículas

Momento lineal e impulso

El momento lineal de una partícula de masa m que se mueve con una velocidad v se define como el producto de la masa por la velocidad

p=mv

Se define el vector fuerza, como la derivada del momento lineal respecto del tiempo

F=dpdt

La segunda ley de Newton es un caso particular de la definición de fuerza, cuando la masa de la partícula es constante.

F=d(mv)dt=mdvdt=ma

Despejando dp en la definición de fuerza e integrando

dp=Fdt  pf−pi=∫titfFdt

A la izquierda, tenemos la variación de momento lineal y a la derecha, la integral que se denomina impulso de la fuerza F en el intervalo que va de t_i a t_f.

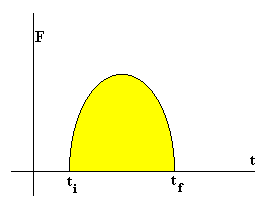Para el movimiento en una dimensión, cuando una partícula  se mueve bajo la acción de una fuerza F, la integral es el área sombreada bajo la curva fuerza-tiempo.

dp=Fdt  pf−pi=∫titfFdt

En muchas situaciones físicas se emplea la aproximación del impulso. En esta aproximación, se supone que una de las fuerzas que actúan sobre la partícula es muy grande pero de muy corta duración. Esta aproximación es de gran utilidad cuando se estudian los choques, por ejemplo, de una pelota con una raqueta o una pala. El tiempo de colisión es muy pequeño, del orden de centésimas o milésimas de segundo, y la fuerza promedio que ejerce la pala o la raqueta es de varios cientos o miles de newtons. Esta fuerza es mucho mayor que la gravedad, por lo que se puede utilizar la aproximación del impulso. Cuando se utiliza esta aproximación es importante recordar que los momentos lineales inicial y final se refieren al instante antes y después de la colisión, respectivamente.

Dinámica de un sistema de partículas

Sea un sistema de partículas. Sobre cada partícula actúan las fuerzas exteriores al sistema y las fuerzas de interacción mutua entre las partículas del sistema. Supongamos un sistema formado por dos partículas. Sobre la partícula 1 actúa la fuerza exterior F₁ y la fuerza que ejerce la partícula 2, F₁₂. Sobre la partícula 2 actúa la fuerza exterior F₂ y la fuerza que ejerce la partícula 1, F₂₁.

Por ejemplo, si el sistema de partículas fuese el formado por la Tierra y la Luna: las fuerzas exteriores serían las que ejerce el Sol (y el resto de los planetas) sobre la Tierra y sobre la Luna. Las fuerzas interiores serían la atracción mutua entre estos dos cuerpos celestes.

Para cada unas de las partículas se cumple que la razón de la variación del momento lineal con el tiempo es igual la resultante de las fuerzas que actúan sobre la partícula considerada, es decir, el movimiento de cada partícula viene determinado por las fuerzas interiores y exteriores que actúan sobre dicha partícula.

dp1dt=F1+F12dp2dt=F2+F21

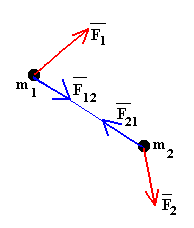
Sumando miembro a miembro y teniendo en cuenta la tercera Ley de Newton, F₁₂=-F₂₁, tenemos que

dp1dt+dp2dt=d(p1+p2)dt=F1+F2dPdt=Fext

Donde P es el momento lineal total del sistema y F_ext es la resultante de las fuerzas exteriores que actúan sobre el sistema de partículas. El movimiento del sistema de partículas viene determinado solamente por las fuerzas exteriores.

Conservación del momento lineal de un sistema de partículas

Considérese dos partículas que pueden interactuar entre sí pero que están aisladas de los alrededores. Las partículas se mueven bajo su interacción mutua pero no hay fuerzas exteriores al sistema.

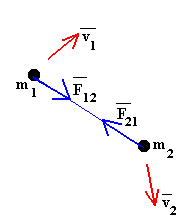La partícula 1 se mueve bajo la acción de la fuerza F₁₂ que ejerce la partícula 2. La partícula 2 se mueve bajo la acción de la fuerza F₂₁ que ejerce la partícula 1. La tercera ley de Newton o Principio de Acción y Reacción establece que ambas fuerzas tendrán que ser iguales y de signo contrario.

F₁₂ +F₂₁ =0

Aplicando la segunda ley de Newton a cada una de las partículas

dp1dt+dp2dt=d(p1+p2)dt=0

El principio de conservación del momento lineal afirma que el momento lineal total del sistema de partículas permanece constante, si el sistema es aislado, es decir, si no actúan fuerzas exteriores sobre las partículas del sistema. El principio de conservación del momento lineal es independiente de la naturaleza de las fuerzas de interacción entre las partículas del sistema aislado

m₁u₁+m₂u₂=m₁v₁+m₂v₂

Donde u₁ y u₂ son las velocidades iniciales de las partículas 1 y 2 y v₁ y v₂ las velocidades finales de dichas partículas.

Colisiones

Se emplea el término de colisión para representar la situación en la que dos o más partículas interaccionan durante un tiempo muy corto. Se supone que las fuerzas impulsivas debidas a la colisión son mucho más grandes que cualquier otra fuerza externa presente.

El momento lineal total se conserva en las colisiones. Sin embargo, la energía cinética no se conserva debido a que parte de la energía cinética se transforma en energía térmica y en energía potencial elástica interna cuando los cuerpos se deforman durante la colisión.

Se define colisión inelástica como la colisión en la cual no se conserva la energía cinética. Cuando dos objetos que chocan se quedan juntos después del choque se dice que la colisión es perfectamente inelástica. Por ejemplo, un meteorito que choca con la Tierra.

En una colisión elástica la energía cinética se conserva. Por ejemplo, las colisiones entre bolas de billar son aproximadamente elásticas. A nivel atómico las colisiones pueden ser perfectamente elásticas.

12m1u21+12m1u21+Q=12m1v21+12m2v22

La magnitud Q es la diferencia entre las energías cinéticas después y antes de la colisión. Q toma el valor de cero en las colisiones perfectamente elásticas, pero puede ser menor que cero si en el choque se pierde energía cinética como resultado de la deformación, o puede ser mayor que cero, si la energía cinética de las partículas después de la colisión es mayor que la inicial, por ejemplo, en la explosión de una granada o en la desintegración radiactiva, parte de la energía química o energía nuclear se convierte en energía cinética de los productos.

Coeficiente de restitución

Se ha encontrado experimentalmente que en una colisión frontal de dos esferas sólidas como las que experimentan las bolas de billar, las velocidades después del choque están relacionadas con las velocidades antes del choque, por la expresión

v1−v2=−e(u1−u2)

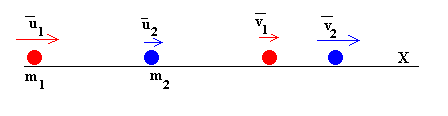
donde e es el coeficiente de restitución y tiene un valor entre 0 y 1. Esta relación fue propuesta por Newton y tiene validez solamente aproximada. El valor de uno es para un choque perfectamente elástico y el valor de cero para un choque perfectamente inelástico.

El coeficiente de restitución es la razón entre la velocidad relativa de alejamiento, y la velocidad relativa de acercamiento de las partículas.

El centro de masa.

El Sistema de Referencia del Centro de Masa (sistema-C) es especialmente útil para describir las colisiones comparado con el Sistema de Referencia del Laboratorio (sistema-L) tal como veremos en próximas páginas.

Movimiento del Centro de Masas

En la figura, tenemos dos partículas de masas m₁ y m₂, como m₁ es mayor que m₂, la posición del centro de masas del sistema de dos partículas estará cerca de la masa mayor.

xcm=m1x1+m2x2m1+m2

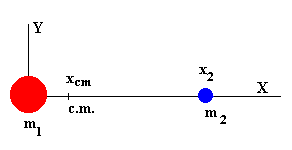
En general, la posición r_cm del centro de masa de un sistema de N partículas es

rcm=∑1Nmiri∑1Nmi

La velocidad del centro de masas v_cm  se obtiene derivando con respecto del tiempo

vcm=∑1Nmivi∑1Nmi=PM

En el numerador figura el momento lineal total y en el denominador la masa total del sistema de partículas.

De la dinámica de un sistema de partículas tenemos que

dPdt=Fext  Mdvcmdt=Fext

El centro de masas de un sistema de partículas se mueve como si fuera una partícula de masa igual a la masa total del sistema bajo la acción de la fuerza externa aplicada al sistema.

En un sistema aislado F_ext=0 el centro de masas se mueve con velocidad constante v_cm=cte.

El Sistema de Referencia del Centro de Masas

Para un sistema de dos partículas

vcm=m1v1+m2v2m1+m2

La velocidad de la partícula 1 respecto del centro de masas es

v1cm=v1−vcm=m2(v1−v2)m1+m2

La velocidad de la partícula 2 respecto del centro de masas es

v2cm=v2−vcm=−m1(v1−v2)m1+m2

En el sistema-C, las dos partículas se mueven en direcciones opuestas.

Momento lineal

Podemos comprobar fácilmente que el momento lineal de la partícula 1 respecto al sistema-C es igual y opuesto al momento lineal de la partícula 2 respecto del sistema-C

p_1cm=m₁v_1cm
p_2cm=m₂v_2cm
p_1cm=-p_2cm

Energía cinética

La relación entre las energías cinéticas medidas en el sistema-L y en el sistema-C es fácil de obtener

Ek=Ekcm+12(m1+m2)v2cm

El primer término, es la energía cinética relativa al centro de masas. El segundo término, es la energía cinética de una partícula cuya masa sea igual a la del sistema moviéndose con la velocidad del centro de masa. A este último término, se le denomina energía cinética de traslación del sistema.

En un sistema de partículas podemos separar el movimiento del sistema en dos partes:

• el movimiento de traslación con la velocidad del centro de masa
• el movimiento interno relativo al centro de masas.

En las siguientes páginas, mostraremos la importancia de centro de masas en la descripción del movimiento de un sistema de dos partículas que interactúan a través de un muelle elástico.

Energía de un sistema de partículas

Supongamos que la partícula de masa m₁ se desplaza dr₁, y que la partícula de masa m₂ se desplaza dr₂, como consecuencia de las fuerzas que actúan sobre cada una de las partículas.

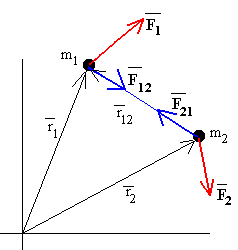El trabajo realizado por la resultante de las  fuerzas que actúan sobre la primera partícula es igual al producto escalar

(F₁+F₁₂)·dr₁

Del mismo modo, el trabajo realizado por la resultante de las fuerzas que actúan sobre la partícula de masa m₂ será

(F₂+F₂₁)·dr₂

Teniendo en cuenta que el trabajo de la resultante de las fuerzas que actúan sobre una partícula modifica la energía cinética de la partícula, es decir, la diferencia entre la energía cinética final y la inicial.

∫(F1+F12)⋅dr1=12m1v21f−12m1v21i∫(F2+F21)⋅dr2=12m2v22f−12m2v22i

Sumando miembro a miembro, podemos escribir el trabajo como suma del trabajo de las fuerzas exteriores más el trabajo de las fuerza interiores o de interacción mutua. Se tiene en cuenta que las fuerzas interiores F₁₂=-F₂₁ soniguales y de sentido contrario

∫F1⋅dr1+∫F2⋅dr2+∫F12(dr1−dr2)=(12m1v21+12m2v22)f−(12m1v21+12m2v22)i

Las fuerzas interiores F₁₂ y F₂₁ realizan trabajo siempre que haya un desplazamiento relativo de la partícula 1 respecto de la 2, ya que dr₁-dr₂=d(r₁-r₂)=dr₁₂

Normalmente, la fuerza F₁₂ es conservativa (es de tipo gravitatorio, eléctrico, muelle elástico, etc.) El trabajo de una fuerza conservativa es igual a la diferencia entre la energía potencial inicial y final.

∫F12⋅dr12=(Ep)i−(Ep)f

Denominando trabajo de las fuerzas exteriores a la suma

Wext=∫F1⋅dr1+∫F2⋅dr2

Tendremos

Wext=(12m1v21+12m2v22+Ep)f−(12m1v21+12m2v22+Ep)i

Entre paréntesis tenemos una cantidad que es la suma de la energía cinética de las dos partículas que forman el sistema y de la energía potencial que describe la interacción entre las dos partículas. A esta cantidad la denominamos energía U del sistema de partículas.

W_ext=U_f-U_i

El trabajo de las fuerzas exteriores es igual a la diferencia entre la energía del sistema de partículas en el estado final y la energía del sistema de partículas en el estado inicial.

Para un sistema de dos partículas, hay una sola interacción de la partícula 1 con la 2 descrita por la fuerza interna  conservativa F₁₂ o por la energía potencial E_p12. La energía del sistema U se escribe

U=12m1v21+12m2v22+Ep12

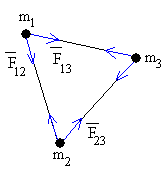Para un sistema formado por tres partículas hay tres interacciones, de la partícula 1 con la 2, la 1 con la 3 y la 2 con la 3, descritas por las fuerzas internas conservativas F₁₂, F₂₃, F₁₃ o por sus correspondientes energías potenciales. La energía del sistema es

U=12m1v21+12m2v22+12m3v23+Ep12+Ep13+Ep23

Sistema aislado

Para un sistema aislado, F_ext=0, el trabajo W_ext de las fuerzas exteriores es cero, la energía U del sistema de partículas se mantiene constante. Para un sistema de dos partículas cuya interacción mutua está descrita por la energía potencial E_p12.

12m1v21+12m2v22+Ep12=cte

La fuerza exterior F_ext es conservativa

El trabajo de la fuerza exterior es igual a la diferencia entre de energía potencial inicial y la final

W_ext=E_pi-E_pf

Tenemos por tanto que U_i+E_pi=U_f+E_pf=cte

Para un sistema de dos partículas bajo la acción de la fuerza conservativa peso, la conservación de la energía se escribirá

12m1v21+12m2v22+Ep12+m1gx1+m2gx2=cte